Are your students struggling with addition? If so, it might be time to introduce them to different strategies for addition.

You might be wondering how different strategies for addition could be life-changing.
When I was younger, I remember being told to do mental math. I understood the concept: mental math is math you do in your head. BUT I did NOT understand how to do it.
This was frustrating!
And, it contributed to a negative view of math that I held onto for a long time.
Consistently having to push through a negative mindset every time I sat down to do math was exhausting. Teaching different addition strategies to students can help make math more accessible to them and help prevent them from having to push through a mental block whenever they do math.
It wasn’t until I was in college that I was formally introduced to a handful of unique addition strategies… And WOW! They are game changers.
Now, as someone who struggled with math for a long time, I absolutely LOVE teaching different ways for students to solve addition problems.
Why Teach Addition Strategies?

1. Mental Math
Teaching addition strategies can increase your students’ abilities to do mental math. The more they practice, the quicker and more confident they will be in their abilities.
2. Creative Problem Solving
Solving addition problems using different strategies for addition helps students look at math more open-mindedly. Knowing there are several ways to solve a problem allows them to try different addition strategies if they get stuck. This is also a great metaphor for problem solving in life outside of math.
3. Number Sense
Number sense is extremely important for students to develop. It will continue to serve them throughout their lives. Understanding how and why numbers work from the beginning will help them to grow and build their knowledge faster and more effectively.
My 3 Favorite Strategies for Addition
1. Partial Sums Addition
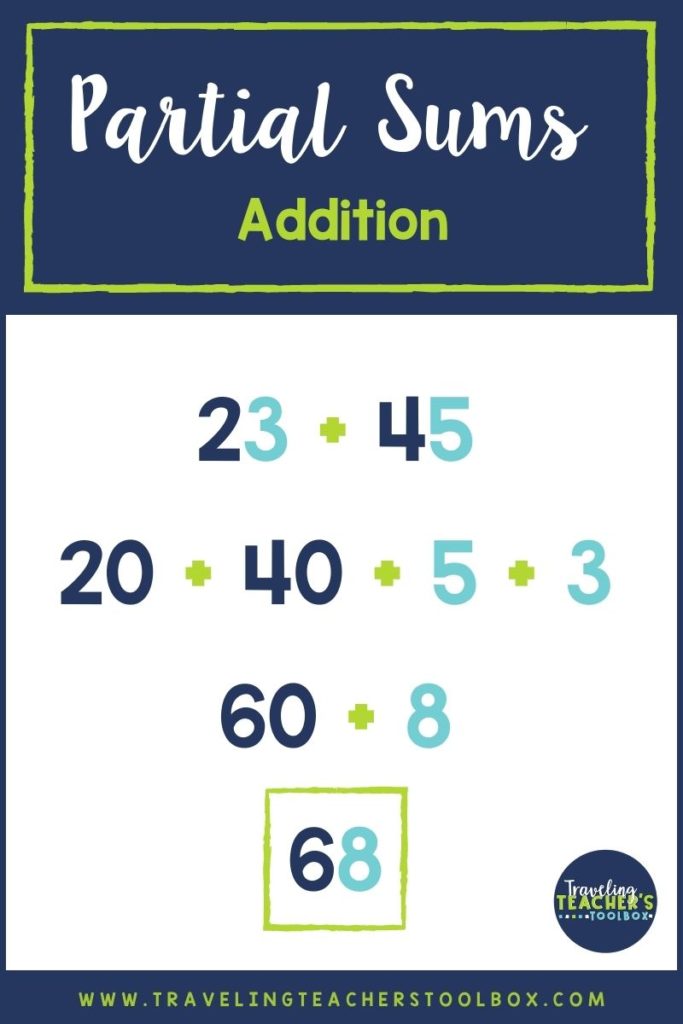
The partial sums addition strategy uses the idea that turning numbers into tens and ones makes math problems more accessible.
Plus, this idea also helps cement the idea of place value in students’ knowledge. Yay! Number sense!
If you have. problem that is 23+45, start by breaking each number into tens and ones.
Now you have 20+3+40+5.
Next, add the tens together: 20+40=60. Then, add the ones together: 3+5=8. Now you have: 50+8=68.
TADA! Your answer is 68!
This strategey also works with numbers that have more digits, as well.
723+221
700+20+3+200+20+1
700+200=900; 20+20=40; and 3+1=4
900+40+4= 944
2. Doubles Plus One, Doubles Minus One Addition

Students commonly memorize doubles facts through 10 early on. For example, many lower elementary kids could tell you that 2+2=4 or that 5+5=10.
Here is an example of a doubles plus one fact:
2+2=4 so 2+3=5.
3 is one more than 2, so the answer to 2+3 will be one more than the answer to 2+2.
Conversely, this works with subtraction as well and is called doubles minus one.
2+2=4 so 2+1=3.
1 is 1 less than 2, so the answer to 2+1 will be one less than the answer to 2+2.
Looking at this with smaller numbers you might be thinking: What’s the point? But when carried over to bigger numbers later on, it will prove to be a very handy skill.
For example, if you asked a kid what 25+26 is off the top of their head, chances are they will give you a confused look. But, if they know doubles plus one, they can quickly determine:
25+25= 50, so 25+26 must be one more than 50.
They can quite quickly and confidently tell you that 25+26 is 51.
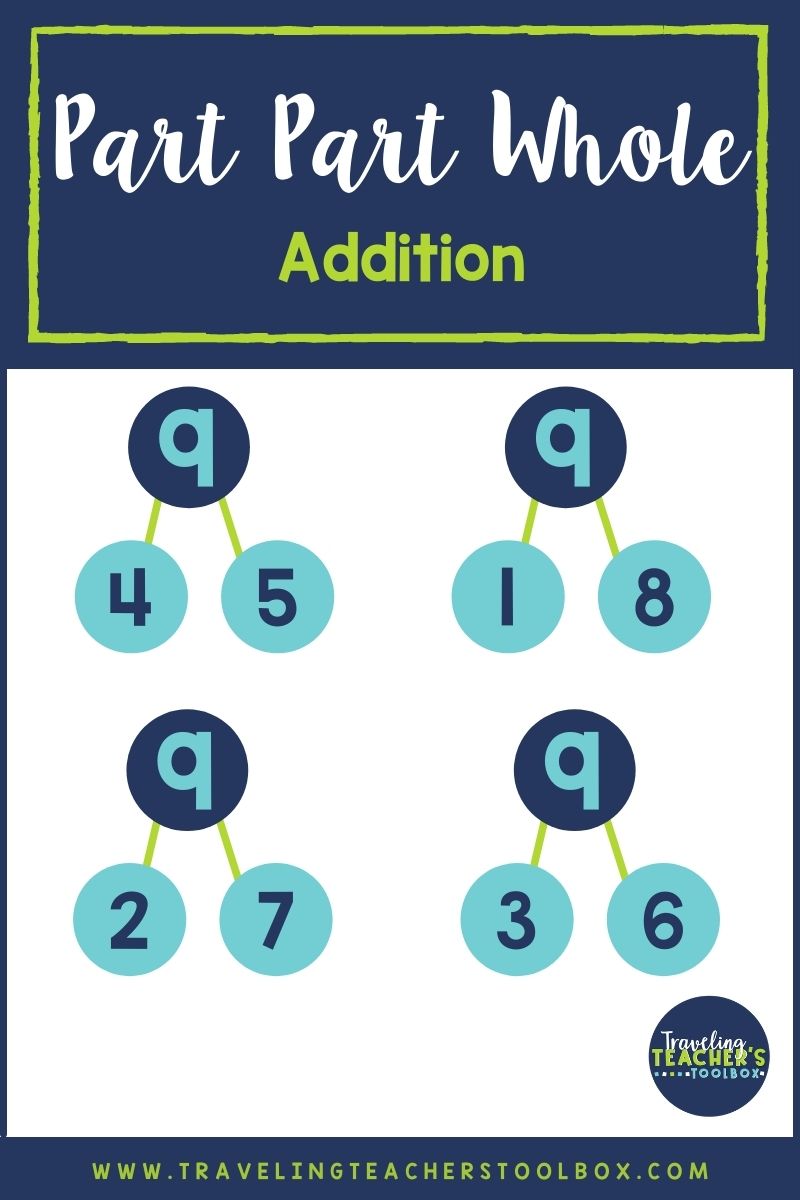
3. Part Part Whole Addition
Part part whole is another important strategy for addition. It allows you to better understand how smaller numbers make up larger numbers and how larger numbers can be broken down into smaller numbers.
Let’s take a look at the number 9. There are several ways you can make 9: 1+8, 7+2, 6+3, and 4+5.
This is fantastic for number sense! But what about mental math?
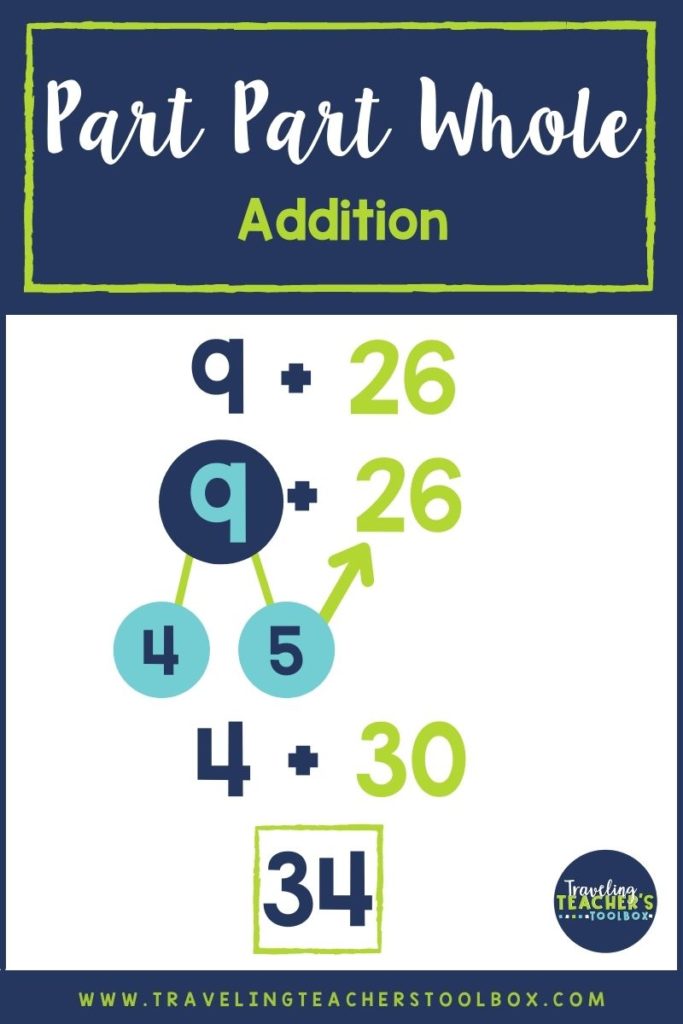
If a student is solving 9+26, they can break 9 into several parts. But which way would work the best?
Start by looking at 26. If 26 could become 30, it would make it much more accessible to work with.
26+4=30
We know 5+4=9, so if we break 9 into 5 and 4, we now have 5+4+26, or 5+30 which is 35.
Therefore, 9+26=35.
Teaching Strategies for Addition
Teaching strategies for addition is great for mental math, creative problem solving, and number sense. They help to make math more accessible for students who are struggling with traditional algorithms or simply don’t naturally understand mental math.
Different methods can work better in different situations or for different students, but by teaching students different addition strategies, you are giving them the tools they need to be successful!
Are you interested in teaching different strategies for addition? Click on the pictures below to shop!
Thanks for stopping by Traveling Teacher’s Toolbox!