The area model of multiplication has been a super controversial topic on social media.
Parents, and even some educators, took social media by storm to complain about how ridiculous the area model of multiplication is.
There were complaints that this method was clunky and that solving problems this way was not as quick as the traditional algorithm.
The traditional algorithm is important to learn and does have a time and place to be used.
However, there are so many benefits to learning the area model of multiplication method. It is a huge disservice to not teach students this method, or to tell them it’s a waste of time to learn.
Why teach the area model of multiplication?
While there are many reasons why this method should be taught, I believe the two most important are organization and number sense.
1. Organization
With the traditional method of multiplication, organization is where most students struggle.
As students multiply each digit, they carry over many numbers. Even when students remember to cross off numbers that they have carried, this still can get overwhelming and cause confusion.
The bigger organization culprit, however, is lining up the rows of products to add at the end.
All it takes is one digit to be off and suddenly the addition becomes ultra confusing. Numbers that are slightly unaligned can be added accidentally in the wrong column or sometimes even in 2 columns, making it hard to find where the error actually lies.
This happens often because students are trying to multiply and organize at the same time. With the area model of multiplication students step themselves up to first multiply and then add.
Although organizational-based errors can still occur, for the most part the area model of multiplication helps students stay more organized.
Thirdly, the zeros. Forgetting to add one zero to the second line, two zeros to the third line, and so on and so forth is not only hard to remember, but confusing. Most students could not tell you why they using those zeros in the first place.
And this brings me to the my second very important reason for teaching this method: number sense!
2. Number Sense
One reason many people are fans of the traditional method is that you can always get the right answer (if you are organized, of course).
However, many students are not able to explain why they got their final answer. While having the right answer is important, it is more important for students to understand why.
Understanding the “why” will help students in the future when they are learning more complicated math. It will also give them confidence in their math abilities.
How to Solve Using the Area Model of Multiplication
The most important thing about using the area model is setting it up correctly. In order to set it up there are some steps to take.
1. Break up each multiple using place value.

2. Place one set of numbers horizontally and stack the other set of numbers to the left.

3. Draw a rectangle underneath the numbers. Turn it into a grid by making lines that separate each of the digits.

4. Once you have drawn the area model, you are ready to multiply. Start by multiplying the numbers on the top with the numbers that coincide with the numbers on the left. Place the final product in the box where the two numbers meet on the grid. Continue doing this until the grid is full.
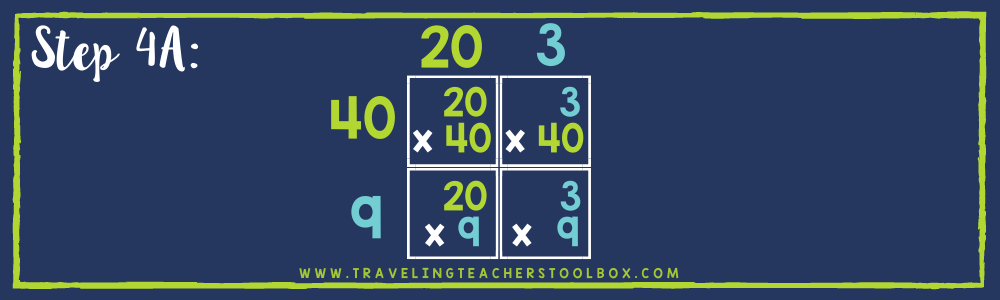

5. Once the grid is completely filled in, take all the numbers inside of it and add them up. The result will be your final answer!

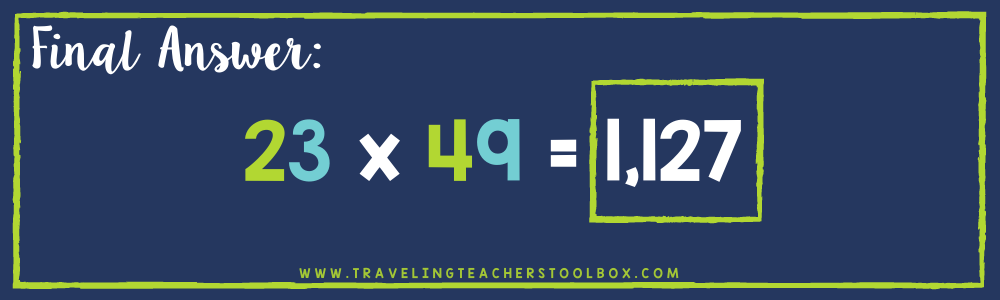
Other Examples of Using the Area Model
Does this work with numbers that have more or less digits than 2?
Yes! Absolutely. Below are examples of 2×1, 2×3, and 4×1 digit problems:



Teaching Area Model of Multiplication?
If you are teaching area model of multiplication and need resources, click on the images below to check out some products I offer in my store!
The image on the left is both a digital and printable resource. The image on the right is for use with Boom Cards. Please make sure that you have an account on the Boom website before purchasing!
Happy teaching and thanks for stopping by Traveling Teacher’s Toolbox!




